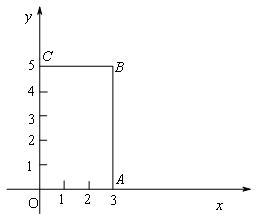
如图，长方形OABC中，O为坐标系的原点，A、C两点的坐标分别为（3，0）、（0，5），点B在第一象限．（1）写出点B的坐标；（2）若过点C的直线CD交AB边于点D，且把长方形OABC的周长分为1：3两部分，求出点D的坐标；（3）如果将（2）中的线段CD向下平移2个单位，得到线段C´D´，试计算四边形OAD´C´的面积．
答案
（1）B（3,5）；
（2）D（3,4）；
（3）四边形OAD´C´的面积为
知识点：坐标与图形变化-平移
（1）点B与点A横坐标相同，与点C纵坐标相同，故B（3,5）．
（2）作出图形，设点D的坐标为（3，m），则（3+5-m）：（8+m）=1:3，则m=4，则D（3,4）
（3）向下平移两个单位得C´（0,3），D´（3,2），则四边形OAD´C´的面积为（2+3）×3÷2=．
略
WORD格式（
