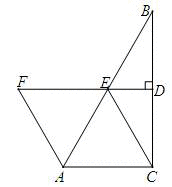
如图，在△ABC中，∠ACB=90°，点E为AB的中点，连接CE，过点E作ED⊥BC于点D，在DE的延长线上取一点F，使AF=CE．(1)证明四边形ACEF是平行四边形；(2)当∠B满足什么条件时，四边形ACEF是菱形，并说明理由．
答案
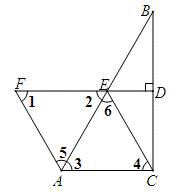
证明：∵∠ACB=90°，BE=AE
∴CE=AE=BE
又∵CE=AF
∴CE=AE＝BE=AF
∴∠1=∠2，∠3=∠4
∵DF⊥BC，∠ACB=90°
∴∠EDB=∠ACD
∴DF∥AC
∴∠2=∠3
∴∠1=∠2=∠3=∠4
∴∠5=∠6
∴AF∥CE
又∵AF=CE
∴四边形ACEF是平行四边形
（2）当∠B=30°时，在Rt△ABC中，
∵四边形ACEF是平行四边形
∴∠B=30°时，四边形ACEF是菱形．
知识点：四边形
略
略
WORD格式（
