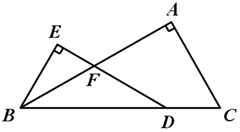
在△ABC中，∠A＝90°，点D在线段BC上，∠EDB＝ $\frac{1}{2}$ ∠C，BE⊥DE，垂足为E，DE与AB相交于点F．
（1）当AB＝AC时（如图）
①∠EBF＝______°；
②究线段BE与FD的数量关系，并加以证明；
（2）当AB＝kAC时（如图），求 $\frac{BE}{FD}$ 的值（用含k的式子表示）．

答案

证明：（1））①∵AB=AC，∠A=90°
∴∠ABC=∠C=45°
∵∠EDB= 12∠C
∴∠EDB=22.5°
∵BE⊥DE
∴∠EBD=67.5°
∴∠EBF=67.5°-45°=22.5°
②如图，过点D作DG∥CA，与BE的延长线相交于点G，与AB相交于H，则∠GDB=∠C，∠BHG=∠A=90°
∵∠EDB= $\frac{1}{2}$ ∠C= $\frac{1}{2}$ ∠GDB=∠EDG
又∵DE=DE，∠DEB=∠DEG=90°
∴△DEB≌△DEG
∴BE=GE= $\frac{1}{2}$ GB
∵∠A=90°，AB=AC
∴∠ABC=∠C=∠GDB
∴HB=HD
∵∠BED=∠BHD=90°，∠BFE=∠DFH
∴∠EBF=∠HDF
∴△GBH≌△FDH
∴GB=FD
∴BE= $\frac{1}{2}$ FD

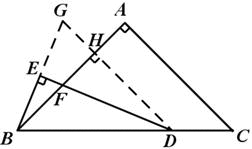
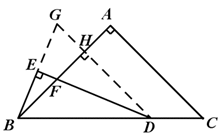
（2）如图，过点D作DG∥CA，与BE的延长线相交于点G，与AB相交于H
同理可证△DEB≌△DEG，BE= $\frac{1}{2}$ GB，∠GHF=∠BHD=90°，
∠EBF=∠HDF，
∴△GBH∽△FDH
∴ $\frac{GB}{FD}$ = $\frac{BH}{DH}$ ，即 $\frac{BE}{FD}$ = $\frac{BH}{2DH}$
又∵DG∥CA
∴△BHD∽△BAC
∴ $\frac{BH}{BA}=\frac{DH}{CA}$ =，即∴ $\frac{BH}{DH}=\frac{BA}{CA}=k$ ，∴ $\frac{BE}{FD}=\frac{k}{2}$

知识点：全等三角形的判定比例的性质相似三角形的判定

（1）①根据题意可判断△ABC为等腰直角三角形，据此即可推断∠C=45°，进而可知∠EDB=22.5°．然后求出∠EBF的度数．
②根据题意证明△BEF∽△DEB，然后利用相似三角形的性质，得到BE与FD的数量关系．
（2）作∠ACB的平分线，得到 ∠C的正切值，然后证明△BEF∽△DEB，利用三角形相似的性质得到BE与FD的数量关系．

不会类比推理解题

下载次数：4

WORD格式（含答案版下载无答案版下载）

<<上一题下一题>>