在△ABC中，BC=2AC，∠DBC=∠ACB，BD=BC，CD交线段AB于点E．
（1）如图1，当∠ACB=90°时，则线段DE、CE之间的数量关系?
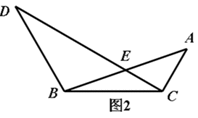
（2）如图2，当∠ACB=120°时，求证：DE=3CE.
答案
证明：（1）∵∠DBC=∠ACB=90°，∴△DBE∽△CAE，∴=
，又∵BD=BC=2AC∴DE=2CE；故答案为DE=2CE．
（2）如图2，∵∠DBC=∠ACB=120°，BD=BC，∴∠D=∠BCD=30°，∴∠ACD=90°，过点B作BF⊥DC于F，则DF=FC，BF= BC，∵AC=
BC，∴BF=AC，又∵∠BFC=∠ACF=90°，∠FEB=∠CEA，∴△BFE≌△ACE，∴FE=CE=
CF，∴DE=3EC；
知识点：全等三角形的判定 等腰三角形的判定与性质 相似三角形的判定与性质
（1）易证△DBE∽△CAE，通过相似比，可得出结论；
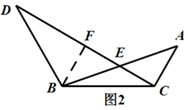
（2）通过作辅助线，过点B作BM⊥DC于M，证明△BME≌△ACE，可证得结论；
第二问容易没有思路
WORD格式（
