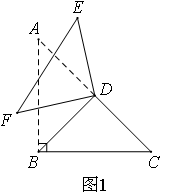
(2011辽宁)如图1,在△ABC中,∠ABC=90°,AB=BC,BD为斜边AC上的中线,将△ABD绕点D顺时针旋转α(0°<α<180°),得到△EFD,点A的对应顶点是E,点B的对应顶点是F,连接BE、CF.
(1)判断BE与CF的位置关系、数量关系,并说明理由;
(2)若连接BF、CE,请直接写出在旋转过程中四边形BFEC能形成哪些特殊四边形;
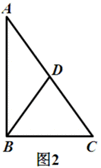
(3)如图2,将△ABC中AB=BC改为AB≠BC时,其他条件不变,直接写出α为多少度时(1)中的两个结论同时成立.
答案
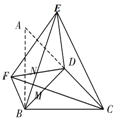
证明:(1)FC=BE,FC⊥BE.
理由如下:
∵ ∠ABC=90°,BD为斜边AC的中线,AB=BC,
∴ BD=AD=CD.
∠ADB=∠BDC=90°.
∵ △ABD旋转得到△EFD,
∴ ∠EDB=∠FDC.
ED=BD,FD=CD.
∴ △BED≌△CFD.
∴ BE=CF.
∴ ∠DEB=∠DFC.
∵ ∠DNE=∠FNB,
∴ ∠DEB+∠DNE=∠DFC+∠FNB.
∴ ∠FMN=∠NDE=90°.
∴ FC⊥BE.
(2)等腰梯形和正方形.
(3)当α=90°(1)两个结论同时成立.
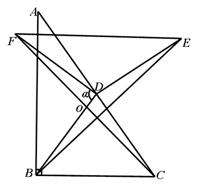
若结论成立,则有BE=FC,BE⊥FC,
BD=FD,DE=DC,
∴△BDE≌△FDC,
∴∠DBE=∠DFC,
∠BOC=∠FOD,
∵BE⊥FC,∴∠DBE+∠BOC=90°
∴∠DFC+∠FOD=90°
∴∠α=90°.
知识点:全等三角形的性质 全等三角形的判定 直角三角形斜边上的中线 等腰直角三角形 几何变换的类型
根据条件先证明△BED≌△CFD.
可以证得BE=CF,BE⊥CF
没有很好的理解题意,对于图形的旋转不会做出相应的图形。不会对三角形全等灵活运用。









