(2011辽宁)在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠DOC=α.将△DOC绕点O按逆时针方向旋转得到△D’OC’(0°<旋转角<90°).连接AC’、BD’,AC’与BD’相交于点M.
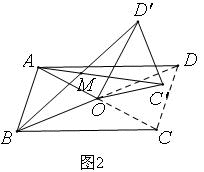
(1)当四边形ABCD是矩形时,如图1,请猜想AC’与BD’的数量关系以及∠AMB与α的大小关系,并证明你的猜想;
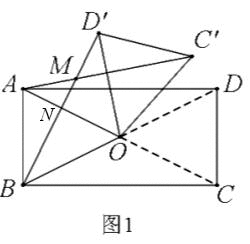
(2)当四边形ABCD是平行四边形时,如图2,已知AC=kBD,请猜想此时AC’与BD’的数量关系以及∠AMB与α的大小关系,并证明你的猜想;
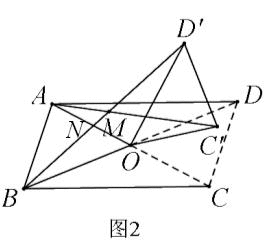
(3)当四边形ABCD是等腰梯形时,如图3,AD∥BC,此时(1)中AC’与BD’的数量关系是否成立?∠AMB与α的大小关系是否成立?不必证明,直接写出结论.


答案
解:(1)AC′=BD′,∠AMB=α
证明:在矩形ABCD中,AC=BD,OA=OC= AC,OB=OD=
BD,
∴OA=OC=OB=OD,
又∵OD=OD′,OC=OC′,
∴OB=OD′=OA=OC′,
∵∠D′OD=∠C′OC,
∴180°-∠D′OD=180°-∠C′OC,
∴∠BOD′=∠AOC′,
∴△BOD′≌△AOC′,
∴BD′=AC′,
∴∠OBD′=∠OAC′,
设BD′与OA相交于点N,
∴∠BNO=∠ANM,
∴180°-∠OAC′-∠ANM=180°-∠OBD′-∠BNO,
即∠AMB=∠AOB=∠COD=α,
综上所述,BD′=AC′,∠AMB=α
(2)AC′=kBD′,∠AMB=α,
证明:在平行四边形ABCD中,OB=OD,OA=OC,
又∵OD=OD′,OC=OC′,
∴OB:OA=OD′:OC′,
∵∠D′OD=∠C′OC,
∴180°-∠D′OD=180°-∠C′OC,
∴∠BOD′=∠AOC′,
∴△BOD′∽△AOC′,
∴BD′:AC′=OB:OA=BD:AC,
∵AC=kBD,
∴AC′=kBD′,
∵△BOD′∽△AOC′,
设BD′与OA相交于点N,
∴∠BNO=∠ANM,
∴180°-∠OAC′-∠ANM=180°-∠OBD′-∠BNO,即∠AMB=∠AOB=α,
综上所述,AC′=kBD′,∠AMB=α,
(3)AC′=BD′成立,∠AMB=α不成立.
知识点:全等三角形的性质 全等三角形的判定 平行四边形的性质 矩形的性质 等腰梯形的性质 规律探索型问题
(1)根据矩形的性质及角之间的关系证明△BOD′≌△AOC′,得出对应边对应角相等,推理即可得出结论;
(2)先进行假设,然后根据平行四边形的性质及相似三角形比例关系即可得出答案;
(3)根据题意并结合图示即可得出结论.
本题主要考查了矩形、平行四边形的性质,全等三角形的判定及性质,相似三角形的判定及性质以及角之间的关系,综合性强,难度较大.










