(2011浙江)以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连结这四个点,得四边形EFGH.
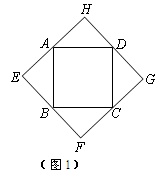
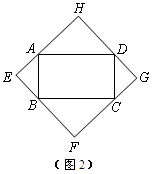
(1)如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;如图2,当四边形ABCD为矩形时,请判断:四边形EFGH的形状(不要求证明);
(2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°),
① 试用含α的代数式表示∠HAE;
② 求证:HE=HG;
③ 四边形EFGH是什么四边形?并说明理由

答案
(1)答:四边形EFGH的形状是正方形.
(2)解:①∠HAE=90°+a,
在平行四边形ABCD中AB∥CD,
∴∠BAD=180°-∠ADC=180°-a,
∵△HAD和△EAB是等腰直角三角形,
∴∠HAD=∠EAB=45°,
∴∠HAE=360°-∠HAD-∠EAB-∠BAD=360°-45°-45°-(180°-a)=90°+a,
答:用含α的代数式表示∠HAE是90°+a.
②证明:∵△AEB和△DGC是等腰直角三角形,
∴AE= BE,DG= CG,
在平行四边形ABCD中,AB=CD,
∴AE=DG,
∵△HAD和△GDC是等腰直角三角形,
∴∠HDA=∠CDG=45°,
∴∠HDG=∠HDA+∠ADC+∠CDG=90°+a=∠HAE,
∵△HAD是等腰直角三角形,
∴HA=HD,
∴△HAE≌△HDG,
∴HE=HG.
③答:四边形EFGH是正方形,
理由是:由②同理可得:GH=GF,FG=FE,
∵HE=HG,
∴GH=GF=EF=HE,
∴四边形EFGH是菱形,
∵△HAE≌△HDG,
∴∠DHG=∠AHE,
∵∠AHD=∠AHG+∠DHG=90°,
∴∠EHG=∠AHG+∠AHE=90°,
∴四边形EFGH是正方形.
知识点:等腰直角三角形 平行四边形的判定与性质 矩形的判定与性质 正方形的判定与性质 规律探索型问题
(1)根据等腰直角三角形得到角都是直角,且边都相等即可判断答案;
(2)①∠HAE=90°+a,根据平行四边形的性质得出,∠BAD=180°-a,根据△HAD和△EAB是等腰直角三角形,得到∠HAD=∠EAB=45°,求出∠HAE即可;
②根据△AEB和△DGC是等腰直角三角形,得出AE= BE,DG= CG,平行四边形的性质得出AB=CD,求出∠HDG=90°+a=∠HAE,证△HAE≌△HDG,即可得出HE=HG;
③由②同理可得:GH=GF,FG=FE,推出GH=GF=EF=HE,得出菱形EFGH,证△HAE≌△HDG,求出∠AHD=90°,∠EHG=90°,即可推出结论.
本题主要考查对正方形的判定,等腰直角三角形的性质,菱形的判定和性质,全等三角形的性质和判定,平行线的性质等知识点的理解和掌握,综合运用性质进行推理是解此题的关键.










