如图：正方形ABCD中有一点P,且PA=1，PB=2，PC=3，求∠APB的度数．

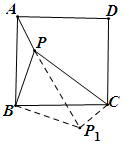
把△APB绕点B旋转到三角形CＰ_１B，则CP₁=AP=1，BP₁=BP=2，∠2=∠1，∠APB=∠CP₁B.
∵ ∠1+∠PBC=90°
∴ ∠2+∠PBC=90°
又BP=BP₁=2
∴ PP₁=，∠BP₁P=45°
在△PP₁C中，PC＝3，PP₁=，P₁C＝1，有ＰＣ²＝ＰＰ_１²＋ＣＰ_１²
∴　∠ＰＰ_１Ｃ＝９０°
∴　∠ＡＰＢ＝∠ＣＰ_１Ｂ＝∠ＢＰ_１Ｐ＋∠ＰＰ_１Ｃ＝４５°＋９０°＝１３５°

通过旋转把条件AP=1，BP=2，CP=3,联系起来。