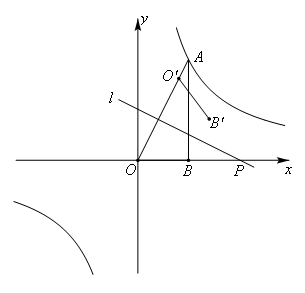
（2011金华）如图，将一块直角三角板OAB放在平面直角坐标系中，B（2，0），∠AOB=60°，点A在第一象限，过点A的双曲线为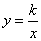
．在x轴上取一点P，过点P作直线OA的垂线l，以直线l为对称轴，线段OB经轴对称变换后的像是O′B′．（1）当点O´与点A重合时，点P的坐标是（ ）；（2）设P（t，0），当O′B′与双曲线有交点时，t的取值范围是（）．
．在x轴上取一点P，过点P作直线OA的垂线l，以直线l为对称轴，线段OB经轴对称变换后的像是O′B′．（1）当点O´与点A重合时，点P的坐标是（ ）；（2）设P（t，0），当O′B′与双曲线有交点时，t的取值范围是（）．
答案
解：（1）由题意可知，OB=2，AB=2
,OA=4，
∴A（2，2）且OP=O′P，
又∵∠AOB=60°，
∴△OO′P是等边三角形，
∴OP=OO′=O′P，
当点O´与点A重合时，OP=OA=AP=4,
点P的坐标是（4,0）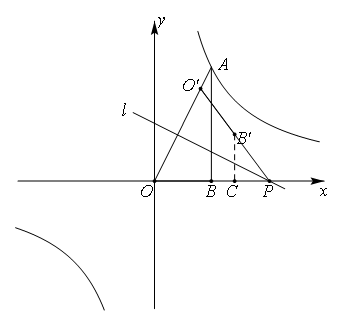
（2）由△OO′P为等边三角形，可知O′B′所在直线为
由点A坐标，易知，k=4
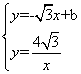
当△=0时，b=±4，是直线与双曲线只有一个交点的情况，也恰好是点O´与双曲线重合的情况。
即当O′B′与双曲线第一象限部分相交时，刚开始时是点O´与点A重合的情况，最终是B′在双曲线上的情况。
在等边三角形OPO′中，P（t，0），过B′作x轴垂线相交于点C，
则在Rt△B′PC中，∠B′PO=60°，B′P=t-2
CP=
, B′C=
OC=OP-CP=
t+1
B′（t+1，）
B′在双曲线上，得
解得t2=20 t1=2
，t2=-2
∴在第一象限，O′B′与双曲线相交时4≤t≤2
同理（也可由对称性）得，在第三象限，O′B′与双曲线相交时-2≤t≤-4
故最终答案为4≤t≤2或-2≤t≤-4。
知识点：反比例函数的图像及性质
略
略
WORD格式（
