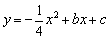（2011河南）如图，在平面直角坐标系中，直线与抛物线交于A、B两点，点A在x轴上，点B的横坐标为－8．（1）求该抛物线的解析式；（2）点P是直线AB上方的抛物线上一动点（不与点A、B重合），过点P作x轴的垂线，垂足为C，交直线AB于点D，作PE⊥AB于点E．①设△PDE的周长为，点P的横坐标为x，求关于的函数关系式，并求出的最大值；②连接PA，以PA为边作图示一侧的正方形APFG．随着点P的运动，正方形的大小、位置也随之改变．当顶点F或G恰好落在y轴上时，直接写出对应的点P的坐标．

答案

解：（1）对于y=x-，当y=0，x=2．当x=-8时，y=-．
∴A点坐标为（2，0），B点坐标为(-8，-)．
由抛物线y=-x²+bx+c经过A、B两点，
得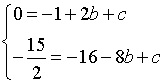
解得b=，c=．
∴y=-x²x+．
（2）①设直线y=x-与y轴交于点M，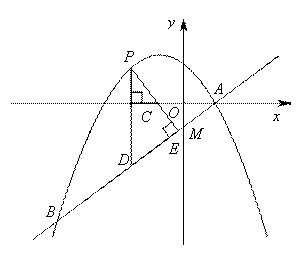

当x=0时，y=-．
∴OM=．
∵点A的坐标为（2，0），
∴OA=2．
∴AM==．
∵OM：OA：AM=3：4：5．
由题意得，∠PDE=∠OMA，∠AOM=∠PED=90°，
∴△AOM∽△PED．
∴DE：PE：PD=3：4：5．
∵点P是直线AB上方的抛物线上一动点，
∵PD⊥x轴，
∴P、D两点横坐标相同，
∴PD=y_P-y_D=x²x+-（x-）=x²x+4
∴l=（x²x+4）=x²x+．
∴l=(x+3)²+15．
∴x=-3时，l_最大=15．
②满足题意的点P有三个，
分别是P₁(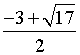，2)，P₂(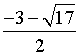，2)，P₃(，)．

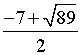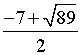知识点：二次函数动点问题  

略

略

下载次数：6

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>