(2011浙江绍兴)抛物线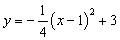 与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.(1)如图1,求点A的坐标及线段OC的长;(2)点P在抛物线上,直线PQ//BC交x轴于点Q,连结BQ.①若含45°角的直角三角板如图2所示放置,其中,一个顶点与点C重合,直角顶点D在BQ上,另一个顶点E在PQ上,求直线BQ的函数解析式;②若含30°角的直角三角板一个顶点与点C重合,直角顶点D在直线BQ上,另一个顶点E在PQ上,求点P的坐标.
与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.(1)如图1,求点A的坐标及线段OC的长;(2)点P在抛物线上,直线PQ//BC交x轴于点Q,连结BQ.①若含45°角的直角三角板如图2所示放置,其中,一个顶点与点C重合,直角顶点D在BQ上,另一个顶点E在PQ上,求直线BQ的函数解析式;②若含30°角的直角三角板一个顶点与点C重合,直角顶点D在直线BQ上,另一个顶点E在PQ上,求点P的坐标.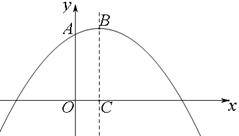 图1
图1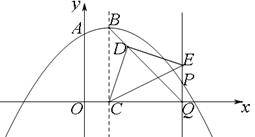 图2
图2
答案
解:(1)把x=0代入抛物线得:y=![]() ,∴点A(0,
,∴点A(0,![]() )
)
抛物线对称轴为:x=1,∴OC=1.
(2)①点B为(1,3),分别过点D作DM⊥x轴于M,DN⊥PQ于点N.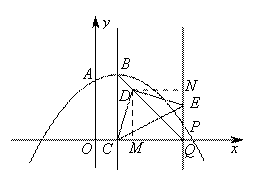
∵PQ∥BC,
∴∠DMQ=∠DNQ=∠MQN=90°,
∴DMQN为矩形.
∵△CDE是等腰直角三角形,
∴DC=DE,∠CDM=∠EDN,
又∵∠CMD=∠END,
∴△CDM≌△EDN,
∴DM=DN,
∴DMQN是正方形,∠BQC=45°.
∴CQ=CB=3,Q为(4,0)
设直线BQ为:y=kx+b,则:![]() ,解得
,解得![]() .
.
∴直线BQ的解析式为:y=-x+4.
②当点P在对称轴右侧时,如图: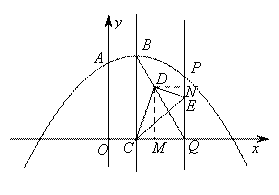
过点D作DM⊥x轴于M,DN⊥PQ于N,
∵∠CDE=90°,
∴∠CDM=∠EDN.
∴△CDM∽△EDN.当∠DCE=30°时,![]() .
.
∵DN=MQ,
∴![]() .
.
∵△DMQ∽△BCQ,
∴![]() ,BC=3,
,BC=3,
∴CQ=![]() .
.
∴Q点为(![]() ,0),P1点为(
,0),P1点为(![]() ,
,![]() ).
).
当∠DCE=60°时,![]() ,
,
CQ=![]() .
.
Q点为(1+![]() ,0),P2点为(1+
,0),P2点为(1+![]() ,
,![]() ).
).
当点P在对称轴左边时,由对称性知:P3点为(![]() ,
,![]() ),P4点为(1-
),P4点为(1-![]() ,
,![]() ).
).
综上所述:P1(![]() ,
,![]() ),P2(1+
),P2(1+![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() ),P4(1-
),P4(1-![]() ,
,![]() ).
).
知识点:二次函数动点问题
略
略







 图1
图1 图2
图2