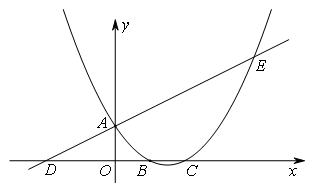
（2009四川眉山）如图，已知直线与轴交于点A，与x轴交于点D，抛物线与直线交于A、E两点，与x轴交于B、C两点，且B点坐标为(1，0)．（1）求该抛物线的解析式；（2）动点P在x轴上移动，当△PAE是直角三角形时，求点P的坐标．

答案

解：（1）∵直线与y轴交于点A,
∴A点为（0,1）
将A（0，1）、B（1，0）坐标代入y=x²+bx+c，
则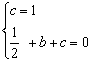，解得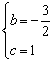
∴抛物线的解折式为y=x²-x+1；
（2）∵抛物线y=x²-x+1与直线交于A、E两点，
则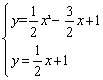，解得（舍去）
∴E点坐标为（4，3）．
（Ⅰ）当A为直角顶点时，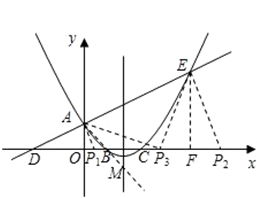

过A作AP₁⊥DE交x轴于P₁点，
设P₁（a，0），易知D点为（-2，0）
由△AOD∽△P₁OA得：=，
即=，
∴a=，
∴P₁点为（，0）．
（Ⅱ）同理，当E为直角顶点时，
过E作EP₂⊥DE交x轴于P₂点，
由△AOD∽△P₂ED得，
=即=，
∴EP₂=，
∴DP₂===，
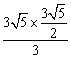∴a==-2=，P₂点坐标为（，0）．
（Ⅲ）当P为直角顶点时，过E作EF⊥x轴于F，
设P₃（b,0）由∠OP₃A+∠FP₃E=90°，得∠OP₃A=∠FEP₃，
又∵∠AOP₃=∠P₃FE=90°，
∴△AOP∽△PFE，
=即=，
解得b₁=3，b₂=1．
∴此时的点P₃的坐标为（1，0）或（3，0），
综上所述，满足条件的P点坐标为（，0）或（1，0）或（3，0）或（，0）．

知识点：二次函数综合题  

略

略

下载次数：7

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>