（2012山东济宁）如图，抛物线y=ax²+bx﹣4与x轴交于A（4，0）、B（-2，0）两点，与y轴交于点C，点P是线段AB的上一动点（端点除外），过点P作PD∥AC，交BC于点D，连接CP．（1）求该抛物线的解析式；（2）当动点P运动到何处时，？（3）当△PCD的面积最大时，求点P的坐标．

答案

解：（1）由题意，得，解得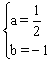
∴抛物线的解析式为y=x²-x-4；
（2）设点P运动到点（x，0）时，有BP²=BD•BC，点C的坐标为（0，-4）．
∵PD∥AC，
∴△BPD∽△BAC，
∴=．
∵BC=，AB=6，BP=x-（-2）=x+2．
∴BD==．
∵BP²=BD•BC，
∴（x+2）²=×，
解得x₁=，x₂=-2（-2不合题意，舍去），
∴点P的坐标是（，0），即当点P运动到（，0）时，BP²=BD•BC；
（3）∵△BPD∽△BAC，
∴，
∴S_△BPD==．S_△PCD=
当x=1时，S_△PCD有最大值为3．即点P的坐标为（1，0）时，△PDC的面积最大．

知识点：二次函数面积问题  

略

略

下载次数：9

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>