（2011年重庆潼南）如图,在平面直角坐标系中，△ABC是直角三角形,∠ACB=90°,AC=BC,OA=1，OC=4，抛物线经过A，B两点，抛物线的顶点为D．（1）求b,c的值；（2）点E是直角三角形ABC斜边AB上一动点(点A、B除外)，过点E作x轴的垂线交抛物线于点F，当线段EF的长度最大时，求点E的坐标；（3）在（2）的条件下：①求以点E、B、F、D为顶点的四边形的面积；②在抛物线上是否存在一点P，使△EFP是以EF为直角边的直角三角形？若存在，求出所有点P的坐标；若不存在，说明理由.

答案

解：（1）如图：∵OA=1，OC=4，
∴BC=AC=AO+CO=5，
∴A点为（﹣1，0），B点为（4，5）．
∵二次函数y=x²+bx+c的图象经过点A（﹣1，0），B（4，5），
∴，解得：．
∴二次函数解析式为y=x²-2x-3．
（2）A点为（﹣1，0），B点为（4，5），
设直线AB解析式为y=kx+b，
则：，解得
∴直线AB的解析式为：y=x+1．设点E（t，t+1），则F（t，t²﹣2t﹣3），
∴EF=（t+1）﹣（t²﹣2t﹣3）=-（t﹣）²+．
∴当t=时，EF取得最大值．
此时E的坐标为（，）．
（3）①如图：顺次连接点E、B、F、D得四边形EBFD．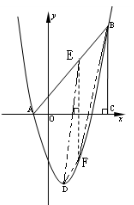

可求出点F的坐标为（，），点D的坐标为（1，﹣4）
S_{四边形EBFD}=S_△BEF+S_△DEF=×（4﹣）+×（﹣1）=．
②如图：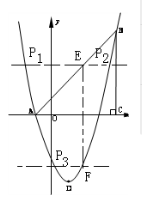

ⅰ）过点E作a⊥EF交抛物线于点P，
设点P（m，m²﹣2m﹣3）则有：m²﹣2m﹣3=，
解得：m₁=，m₂=，
∴P₁（，），P₂（，）．
ⅱ）过点F作b⊥EF交抛物线于P₃，
设P₃（n，n²﹣2n﹣3）则有：n²﹣2n﹣3=﹣，
解得：n₁=，n₂=（与点F重合，舍去）
∴P₃（，﹣），
综上所述：能使△EFP是以EF为直角边的直角三角形的P点坐标有：P₁（，），P₂（，），P₃（，﹣）．

知识点：二次函数综合题  

略

略

下载次数：7

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>