（2012湖南株洲）如图，一次函数分别交y轴、x轴于A、B两点，抛物线过A、B两点.（1）求这个抛物线的解析式；（2）作垂直x轴的直线x=t，在第一象限交直线AB于M，交这个抛物线于N.求当t取何值时，MN有最大值？最大值是多少？（3）在（2）的情况下，以A、M、N、D为顶点作平行四边形，求第四个顶点D的坐标.
备用图

答案

解：（1）∵y=-x+2分别交y轴、x轴于A、B两点，
∴A、B点的坐标为：A（0，2），B（4，0）
∵抛物线过A、B两点，
则：，解得，
∴抛物线解析式为：y=-x²+x+2．
（2）如答图1，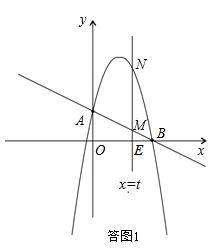
设MN交x轴于点E，则E（t，0），BE=4-t．
∵tan∠ABO===，
∴ME=BE•tan∠ABO=（4-t）×=2-t．
又N点在抛物线y=-x²+x+2上，且点横坐标是:x=t，
∴N点纵坐标：NE=-t²+t+2，
∴MN=NE-ME=-t²+t+2-（2-t）=-t²+4t．
∴当t=2时，MN有最大值4．
（3）由（2）可知，A（0，2），M（2，1），N（2，5）．以A、M、N、D为顶点作平行四边形，D点的可能位置有三种情形，如图2所示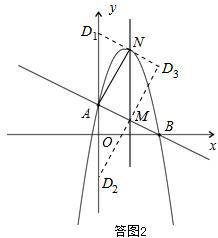

（i）当D在y轴上时，设D的坐标为（0，a）由AD=MN，得=4，解得a₁=6，a₂=-2，
∴D₁点为（0，6），D₂点为（0，-2）．
（ii）当D不在y轴上时，由图可知D为D₁N与D₂M的交点．
设直线D₁N为：y=kx+b,则
，解得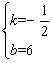
∴直线D₁N解析式为：y=-x+6．
设直线D₂M为y=kx+b,则
，解得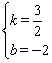
∴直线D₂M解析式为：y=x-2．
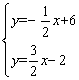联立，得
∴D₃点为（4，4）
综上所述，满足条件的D点坐标为（0，6），（0，-2）或（4，4）．

知识点：二次函数-平行四边形的存在性  

略

略

下载次数：10

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>