（2010河南）在平面直角坐标系中，已知抛物线经过A
，B
，C
三点．（1）求抛物线的解析式；（2）若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S．求S关于m的函数关系式，并求出S的最大值．（3）若点P是抛物线上的动点，点Q是直线
上的动点，判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．
，B
，C
三点．（1）求抛物线的解析式；（2）若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S．求S关于m的函数关系式，并求出S的最大值．（3）若点P是抛物线上的动点，点Q是直线
上的动点，判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．
答案
解：（1）设抛物线的解析式为y=ax²+bx+c（a≠0）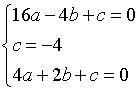
解得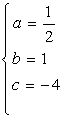
∴抛物线的解析式为y=
x²+x-4
（2）过点M作MD⊥x轴于点D，设M点的坐标为（m，n）（-4＜m＜0）
则AD=m+4，MD=-n，n=m²+m-4，
∴S=S△AMD+S梯形DMBQ-S△ABO=(m+4)(-n)+(-n+4)(-m)-×4×4=-2n-2m-8=-2 (m2+m-4)-2m-8=-m2-4m=
∴S最大值=4.
（3）①当OB为边时，根据平行四边形的性质知PQ∥OB，则Q（x，-x），P（x，x²+x-4）．
由PQ=OB，得|-x-（x²+x-4）|=4，解得x=0（不合题意，舍去），-4，-2-2
，-2+2．
由此可得Q（-4，4）或（-2+2，2-2）或（-2-2，2+2）
②当OB为对角线时，那么P、Q的横坐标互为相反数（若P的横坐标为x，则Q的横坐标为-x），
设P（x，x²+x-4），Q（-x，x）.
由P、O的纵坐标差的绝对值等于Q、B纵坐标差的绝对值，
得x²+x-4=-4-x或x²+x-4=4+x
解得x=0（不合题意，舍去）或-4或4．
由此可得Q（-4，4）或（4，-4）
故满足题意的Q点的坐标有四个，分别是（-4，4），（4，-4）（-2+2，2-2），（-2-2，2+2）
知识点：二次函数-平行四边形的存在性
略
略
WORD格式（
