如图,在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A爬行,经过t分钟后,它们分别爬行到D、E处,请问(1)在爬行过程中,CD和BE始终相等吗?
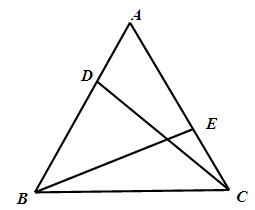
(2)如果将原题中的“由A向B和由C向A爬行”,改为“沿着AB和CA的延长线爬行”,EB与CD交于点Q,其他条件不变,如图(2)所示,蜗牛爬行过程中∠CQE的大小保持不变.请利用图(2)情形,求证:∠ CQE =60°;
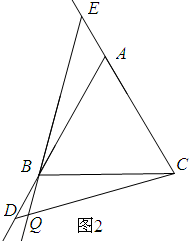
(3)如果将原题中“由C向A爬行”改为“沿着BC的延长线爬行,连接DE交AC于F”,其他条件不变,如图(3),则爬行过程中,DF始终等于EF是否正确.
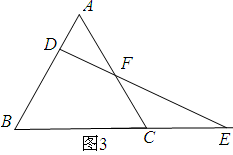
答案
解:(1)CD与BE相等。
证明:由于两只蜗牛同时以相同的速度爬行,所以路程相同,即AD=CE。
∵△ABC是等边三角形,∴AC=BC,∠A=∠BCE;
在△ADC与CEB中
∴△ADC≌△CEB
∴CD=BE
由于t 为任意时刻,所以当t 为任意值时都有CD=BE,即CD和BE始终相等。
(2)证明:由于两只蜗牛以相同速度同时出发,所以路程相同,即AD=CE
∵△ABC是等边三角形
∴AB=AC,∴AD-AB=CE-AC,即AE=BD
而由△ABC是等边三角形还可得
AB=CB,∠CBD=∠BAE=120°
在△EAB和△DBC中
∴△EAB≌△DBC(SAS)
∴∠1=∠4,而∠2=∠3
∴∠1+∠2=∠3+∠4
又∠CQE=∠1+∠2,∠5=∠3+∠4=60°
∴∠CQE=∠5=60°。

(3)正确。
证明:如图,过点D作DG∥BE交AC于点G。
由于△ABC为等边三角形,∴∠A=∠B=60°
∵DG∥BE∴∠1=∠2,∠ADG=∠B=60°,∴△ADG为等边三角形
∴AD=DG
由于蜗牛速度和出发时间相同,所以路程相等,即AD=CE
∴DG=CE
在△DGF和△ECF中
∴△DGF≌△ECF
∴DF=EF
而由于运动时间是任意的,故DF是中等于EF。
知识点:运动变化型问题
当看到动点问题时,首先要分析动点的起点和终点。然后用路程=速度×时间来表示出线段的长度。而在运动过程中考虑线段的变化情况。寻找等量关系证明三角形全等。
将线段表示出来时有一定的难度。










