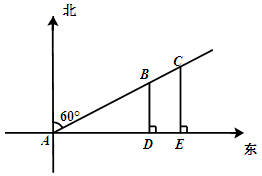
如图，一条渔船某时刻在位置A观测灯塔B、C（灯塔B距离A处较近），两个灯塔恰好在北偏东60°的方向上，渔船向正东方向航行1小时45分钟之后到达D点，观测到灯塔B恰好在正北方向上，已知两个灯塔之间的距离是12海里，渔船的速度是16海里/时，又知在灯塔C周围18.6海里内有暗礁，问这条渔船按原来的方向继续航行，有没有触礁的危险?

1小时45分= 小时，
在Rt△ABD中，
AD=16× =28（海里），
∠BAD=90°-60°=30°，
∵cos30°= ，
∴AB= AD/cos30°= （海里），
AC=AB+BC=  +12（海里）
在Rt△ACE中，
sin30°= ，
∴CE=AC•sin30°=（ +12）×≈22.2（海里），
∵22.2＞18.6，
∴这条渔船按原来的方向继续航行没有触礁危险．

对于触礁概念不理解