(2007北京)如图,已知△ABC.
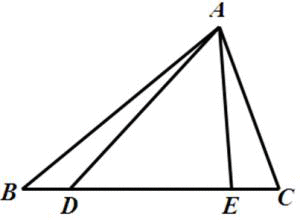
(1)请你在BC边上分别取两点D、E(BC的中点除外),连结AD、AE,写出使此图中只存在两对面积相等的三角形的相应条件,并表示出面积相等的三角形;
(2)请你根据使⑴成立的相应条件,证明AB+AC>AD+AE.
答案
(1)如图1,相应的条件就应该是BD=CE≠DE,
这样,三角形ABD和AEC的面积相等,由于BD=CE,因此BE=CD,那么三角形ADC和三角形ABE的面积就相等.
(2)证明:如图2,分别过点D、B作CA、EA的平行线,两线相交于F点,DF于AB交于G点.
∴∠ACE=∠FDB,∠AEC=∠FBD
在△AEC和△FBD中,又CE=BD,
∴△AEC≌△FBD,
∴AC=FD,AE=FB,
在△AGD中,AG+DG>AD,
在△BFG中,BG+FG>FB,
∴AG+DG-AD>0,BG+FG-FB>0,
∴AG+DG+BG+FG-AD-FB>0,
即AB+FD>AD+FB
∴AB+AC>AD+AE.
(1)由于都是以BC所在边为底,因此边上的高都相等.要两个三角形的面积相等,只需在BC上找出两条相等线段即可;
(2)可通过构建全等三角形来求解.
分别过点D、B作CA、EA的平行线,两线相交于F点,DF于AB交于G点.
那么我们不难得出△AEC≌△FBD,此时AC=DF,AE=BF,那么只需在三角形BFG和ADG中找出它们的关系即可.
本题考查了三角形面积的求法,全等三角形的判定以及三角形三边的关系.
本题(2)中通过构建全等三角形将已知和所求条件转化到相关的三角形中是解题的关键.









