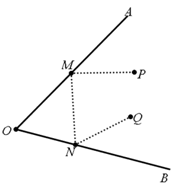
已知锐角∠AOB，在∠AOB内有P，Q两点，在OA边上找点M，在OB边上找点N，使得PM+MN+QN的值最小．
答案
做点P关于OA的对称点P'，点Q关于OB的对称点Q','连接P'M,MN,NQ'。所以PM+MN+QN=P'M+MN+NQ',因为点M，N分别在OA上，OB，连接P',Q',由两点之间线段最短，当M,N分别是P'Q'与OA,OB的交点时，PM+MN+QN最小。
知识点：化归转换思想
首先找到点P关于OA，点Q关于OB的对称点，把线段PM，QN等量代换为P'M,Q'N。然后利用两点之间线段最短，找出P'Q'与OA,OB的交点，即是要找的M,N点。
利用转化的思想，巧妙地线段转移出去。
WORD格式（
