在△ABC中，∠BAC＝120°，AB＝AC，在BC上存在两点M、N，满足∠MAN＝60°，且BM＝5，NC＝8，求MN．

答案

∵∠BAC=120°，AB=AC
∴∠ABC=∠ACB=30°
如图，作∠BAD=∠CAN，且使AD=AN，连接BD

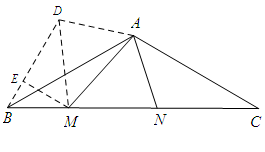
得△ABD≌△ACN
∴BD=NC=8，∠DBA=∠ACB=30°
∴∠DBM=60°
∵∠MAN=60°
∴∠BAM+∠CAN=60°
∴∠DAB+∠BAM=∠DAM=60°
又∵AM=AM，AD=AN
∴△AMD≌△AMN
∴DM=MN
作ME⊥BD于E，则ME=BM·sin60°=5×=，BE=，DE=
∴MN=DM==7

知识点：全等三角形的判定  勾股定理  旋转的性质  

略

对于二倍角的问题掌握不熟练

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>