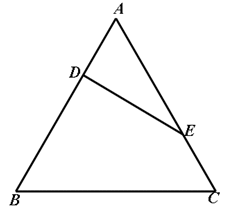
如图，△ABC中，AB＝AC，D、E是AB、AC上的点且AD＝CE．求证：2DE≥BC．
答案
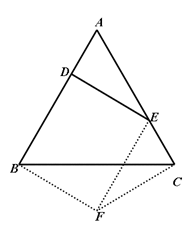
过B作BF∥DE且BF=DE，连接EF，则四边形DEFB为平行四边形，且DB=EF=AE。
因为EF∥AB，则∠CEF=∠A，又因为AD=CE，所以△ADE≌△ECF，则DE=CF，在△BFC中，BF+CF>BC，及2BD>BC，当DE为中位线时，2DE=BC，所以2DE≥BC。
知识点：平移的性质
过B作BF∥DE且BF=DE，连接EF，则四边形DEFB为平行四边形，且DB=EF=AE。
因为EF∥AB，则∠CEF=∠A，又因为AD=CE，所以△ADE≌△ECF，则DE=CF，在△BFC中，BF+CF>BC，及2BD>BC，当DE为中位线时，2DE=BC，所以2DE≥BC。
这道题目考查了线段的转移，把DE转移到三角形BCF中，利用两边之和大于第三边。
WORD格式（
