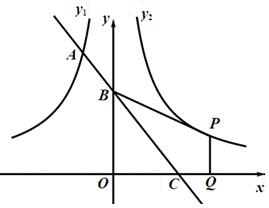
（2011四川）如图，一次函数的图象与反比例函数(x＜0）的图象相交于A点，与y轴、x轴分别相交于B、C两点，且C（2，0)．当x＜-1时，一次函数值大于反比例函数的值，当x＞-1时，一次函数值小于反比例函数值．
 （1）求一次函数的解析式；
 （2）设函数  (x＞0)的图象与(x＜0)的图象关于y轴对称．在 (x＞0)的图象上取一点P（P点的横坐标大于2)，过P作PQ⊥x轴，垂足是Q，若四边形BCQP的面积等于2，求P点的坐标．

答案

（1）∵x＜-1时，一次函数值大于反比例函数值，当x＞-1时候，一次函数值小于反比例函数值．
∴A点的横坐标是-1，
∴A（-1，3），
设一次函数的解析式为y=kx+b，因直线过A、C，
则
解之得 ，
∴一次函数的解析式为y=-x+2；
（2）∵的图象与(x＜0)的图象关于y轴对称，
∴（x＞0），
∵B点是直线y=-x+2与y轴的交点，
∴B（0，2），
设p（n， ），n＞2，
S_{四边形BCQP}=S_{四边形OQPB}-S_△OBC=2，
∴（2+ ）n- ×2×2=2，
n= ，
∴P（ ，）．

知识点：反比例函数的图象  反比例函数的应用  反比例函数综合题  

（1）根据x＜-1时，一次函数值大于反比例函数值，当x＞-1时候，一次函数值小于反比例函数值得到点A的坐标，利用待定系数法求函数的解析式即可；
（2）求得B点的坐标后设出P点的坐标，利用告诉的四边形的面积得到函数关系式求得点P的坐标即可．

此题主要考查反比例函数的性质，注意通过解方程组求出交点坐标．同时要注意运用数形结合的思想．

下载次数：2

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>