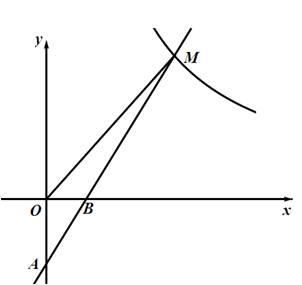（2011山东）如图，一次函数 $y=k_{1}x+b$ 的图象经过A（0，-2），B(1,0)两点，与反比例函数 $y=\frac{k_{2}}{x}$ 的图象在第一象限内的交点为M，若△OBM的面积为2．
（1）求一次函数和反比例函数的表达式；
（2）在x轴上是否存在点P，使AM⊥MP？若存在，求出点P的坐标；若不存在，说明理由．

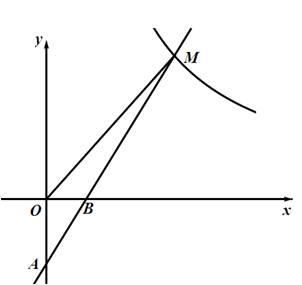
答案

（1）分别把A(0，-2)，B(1,0)代入y=k₁x+b，可解得k₁=2，b=-2，所以y=2x-2。
设M（m ，2m-2），因为△ABC的面积是2，所以1×（2m-2）× $\frac{1}{2}$ =2，所以m=3，所以M（3,4），代入反比例函数y= $\frac{k_{2}}{x}$ ，得k₂=12，所以y= $\frac{12}{x}$ 。
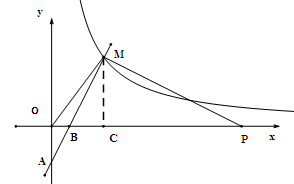
（2）设存在P使得AM⊥MP，P(p，0)，过M做MC⊥x轴于C点，因为M(3，4)，所以MC=4，OC=3，BC=2，BM=2 $\sqrt{5}$ ，因为∠MBC=∠PBM，∠BCM=∠BMP，所以△BCM∽△BMP，所以 $\frac{BC}{BM}$ = $\frac{BM}{BP}$ ，即 $\frac{2}{2\sqrt{5}}$ = $\frac{2\sqrt{5}}{p-1}$ ，解之得p=11，所以存在P(11，0)。