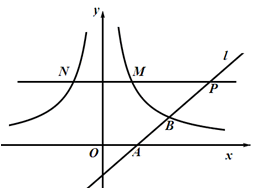
（2011江苏）如图，直线l经过点A（1，0），且与曲线 y=（x＞0）交于点B（2，1）．过点P（p，p-1）（p＞1）作x轴的平行线分别交曲线 y=   （x＞0）和y= （x＜0）于M、N两点．
 （1）求m的值及直线l的解析式；
（2）若点P在直线y=2上，求证：△PMB∽△PNA；
 （3）是否存在实数p，使得S_△AMN=4S_△APM？若存在，请求出所有满足条件的p的值；若不存在，请说明理由．

答案

(1)把B（2,1）代入y=，得m=2，设直线l的表达式为：y=kx+b，将A(1，O)，B（2,1）代入解得k=1，b=-1，∴y=x-1
(2)∵点P在直线y=2上，∴P(3，2)，M(1，2)，N（-1，2），∴PM=2，PN=4，∵A(1，O)，B（2,1），∴PB=，PA=2，∴=，又因为∠MPB=∠NPA，∴△PMB∽△PNA。
（3）设存在实数p，使得S_△AMN=4S_△APM，∴MN=4PM，M(，p-1)，N(-，p-1)，∴①当1＜p＜2时，MN=，PM= -p，∴=4×（-p），解之得p₁=，p₂=（舍去）。②当2≤p时，MN=，PM=p- ，∴=4×（p- ），解之得p₃=，p₄=(舍去)。综合①，②得存在p=或p=，使得S_△AMN=4S_△APM

知识点：待定系数法求一次函数解析式  反比例函数综合题  相似三角形的判定  

（1）直接利用待定系数法来求。
（2）利用两边对应成比例，且夹角相等来证明。
（3）根据等高的三角形面积之比等于底边之比，得MN=4PM，然后分情况讨论P点可能的位置，是否符合要求。

点P的位置需要分情况讨论，不符合题意的值要舍去。

下载次数：12

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>