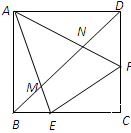
如图，在正方形ABCD中，E、F分别是边BC、CD上的点，满足△CEF的周长等于正方形ABCD的周长的一半，AE、AF分别与对角线BD交于M、N，
（1）线段BE、EF、DF之间存在什么样的数量关系？
（2）你能猜出∠EAF的度数吗？
（3）连接BD，试问线段BM、MN、DN能否构成三角形的三边长？
若能，指出三角形的形状，并给出证明；若不能，请说明理由．

（1）∵“△ECF的周长等于正方形ABCD的周长的一半
∴FE=DF+BE
（2）延长EB至G，截BG=DF，连接AG
则△ABH≌△ADF
∴AF=AG , ∠FAG=90°
∵FE=DF+BE
∴FE=EG
∴△AFE≌△AEG （SSS）
∴∠FAE=∠EAG
∴∠FAE=45°
（3）线段BM、MN、DN能构成直角三角形的三边长．理由如下：
把△ADF绕点A顺时针旋转90°得到△ABP，点N的对应点为Q，
∴BP=DF，BQ=DN，AF=AP，
∵△CEF的周长等于正方形ABCD的周长的一半，
∴EF=BE+DF，
∴EF=EP，
∴△AEF≌△AEP，而AQ=AN，
∴△AMQ≌△AMN，
∴MN=QM，
而∠ADN=∠QBA=45°，∠ABD=45°，
∴∠QBN=90°，
∴BQ²+BM²=QM²，
∴BM²+DN²=MN²．

不能根据题意准确做出辅助线，进而把线段转移到一个三角形中，找到线段之间的关系