(2011绥化)在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G连接EG,CG,如图1,易证EG=CG且EG⊥CG.
(1)将△BEF绕点B逆时针旋转90°,如图2,则线段EG和CG有怎样的数量关系和位置关系?请直接写出你的猜想.
(2)将△BEF绕点B逆时针旋转180°,如图3,则线段EG和CG有怎样的数量关系和位置关系?请写出你的猜想.并加以证明.

答案
解:(1)EG=CG,EG⊥CG.
(2)EG=CG,EG⊥CG.
证明:延长FE交DC延长线于M,连MG.
∵∠AEM=90°,∠EBC=90°,∠BCM=90°,
∴四边形BEMC是矩形.
∴BE=CM,∠EMC=90°,
由图(1)可知,△BEF为等腰直角三角形,∴BE=EF,
∴EF=CM.
∵∠EMC=90°,FG=DG,
∴MG= FD=FG.
∵BC=EM,BC=CD,
∴EM=CD.
∵EF=CM,
∴FM=DM,
∴∠F=45°.
又FG=DG,
∠CMG= ∠EMC=45°,
∴∠F=∠GMC.
∴.
∴EG=CG,∠FGE=∠MGC.
∵∠FMC=90°,MF=MD,FG=DG,
∴MG⊥FD,
∴∠FGE+∠EGM=90°,
∴∠MGC+∠EGM=90°,
即∠EGC=90°,
∴EG⊥CG.
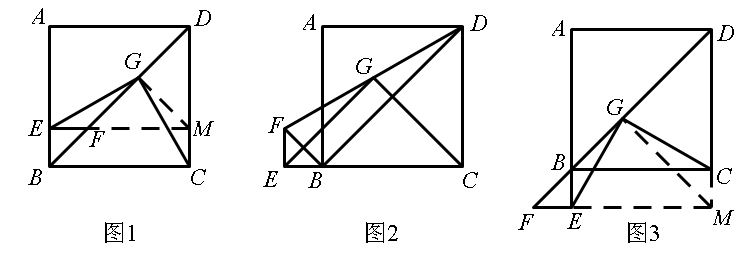
从图(1)中寻找证明结论的思路:延长FE交DC延长线于M,连MG.构造出.易得结论;在图(2)、(3)中借鉴此解法证明.
对旋转的性质及全等三角形的判断和性质不熟练,不会构造全等的三角形。








