如图1，已知等腰直角△ABC中，BD为斜边上的中线，E为DC上的一点，且AG⊥BE于G，AG交BD于F．（1）求证：AF=BE（2）如图2，若点E在DC的延长线上，其它条件不变，①的结论还能成立吗？若不能，请说明理由；若能，请予以证明．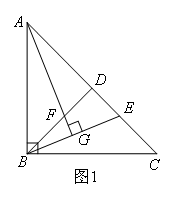
答案
（1）证明：
∵等腰直角△ABC中,BD为斜边上的中线
∴BD⊥AD，BD=AD，∠ABD=∠C=45°
∵AG⊥BE
∴∠BAF+∠ABG=90°，
∵∠CBE+∠ABG=90°
∴∠BAF=∠CBE∵BD=AD，∠ABD=∠C
∴△ABF≌△BCE∴AF=BE
（2）成立，理由：
∵等腰直角△ABC中,BD为斜边上的中线
∴BD⊥AD，AB=BC，∠ABD=∠C=45°
∴∠ABF=∠BCE=135°
∵AG⊥BE
∴∠GAB+∠ABG=90°
∵∠ABG+∠CBE=90°
∴∠GAB=∠CBE
∴△ABF≌△BCE
∴AF=BE
知识点：全等三角形
略
略
WORD格式（
