如图1,在正方形ABCD和正方形CGEF(CG>BC)中,点B,C,G在同一直线上,点M是AE的中点.(1)探究线段MD,MF的位置及数量关系,并证明.(2)将图1中的正方形CGEF绕点C顺时针旋转,使正方形CGEF的对角线CE恰好与正方形ABCD的边BC在同一条直线上,如图2,原问题中的其他条件不变,则(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.(3)若将图1中的正方形CGEF绕点C顺时针旋转任意角度,如图3,原问题中的其他条件不变,则(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.

答案
解(1)MD⊥MF且MD=MF证明:延长DM交EF于点N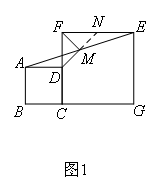
∵AD∥EF
∴∠MAD=∠MEN
∵∠AMD=∠EMN,AM=EM
∴△AMD≌△EMN
∴AD=EN,DM=NM
∵EF=CF,AD=CD
∴EF-EN=CF-AD=CF-CD,即:FD=FN
∴ △DFN是等腰直角三角形
∴MD⊥MF且MD=MF
(2)不发生改变证明:延长DM交CE于点N,连接DF、FN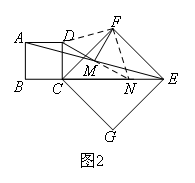
∵AD∥CE
∴∠MAD=∠MEN
∵∠AMD=∠EMN,AM=EM
∴△AMD≌△EMN
∴AD=EN,DM=NM
∵AD=CD
∴EN=CD
∵FE=FC,∠FEN=∠FCD
∴△FEN≌△FCD
∴FN=FD,∠EFN=∠CFD
∴∠DFN=∠EFC=90°
∴ △DFN是等腰直角三角形
∴MD⊥MF且MD=MF
(3)不发生改变证明:过点E做AD的平行线交DM的延长线于点N,连接DF、FN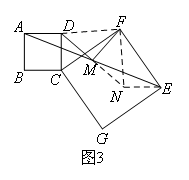
∵AD∥EN
∴∠MAD=∠MEN
∵∠AMD=∠EMN,AM=EM
∴△AMD≌△EMN
∴AD=EN,DM=NM
∵AD=CD
∴EN=CD
∵CD⊥NE,EF⊥CF
∴∠FEN=∠FCD
∵FE=FC
∴△FEN≌△FCD
∴FN=FD,∠EFN=∠CFD
∴∠DFN=∠EFC=90°
∴ △DFN是等腰直角三角形
∴MD⊥MF且MD=MF
知识点:四边形中的类比探究
略
略








