如图，已知等边三角形ABC中，点D，E，F分别为边AB，AC，BC的中点，M为直线BC上一动点，△DMN为等边三角形（点M的位置改变时，△DMN也随之整体移动）．
（1）如图①，当点M在点B左侧时，请你判断EN与MF有怎样的数量关系？点F是否在直线NE上？写出结论并证明；
（2）如图②，当点M在BC上时，其它条件不变，（1）的结论中EN与MF的数量关系是否仍然成立？若成立，请利用图②证明；若不成立，请说明理由；
（3）若点M在点C右侧时，请你在图③中画出相应的图形，并判断（1）的结论中EN与MF的数量关系是否仍然成立？若成立，请利用图③证明；若不成立，请说明理由．
答案
解（1）EN＝MF，点F在直线NE上证明：如图，连接DE、DF，则DE、DF是三角形的中位线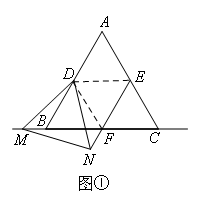
∴DE＝
BC，DF＝AC，△BDF、△ADE都是等边三角形
∴DE＝DF，∠EDF＝60°
∵△DMN为等边三角形
∴∠MDN＝60°，DM＝DN
∴∠MDN+∠NDF＝∠EDF+∠NDF，
即：∠MDF＝∠NDE
∴△NDE≌△MDF
∴EN＝MF，∠DEN＝∠DFM＝60°
∴∠CEN＝60°
∴点F在直线NE上
（2）成立证明：如图，连接DE、DF，则DE、DF是三角形的中位线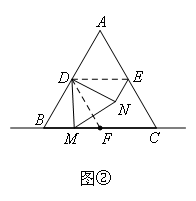
∴DE＝BC，DF＝AC，△BDF、△ADE都是等边三角形
∴DE＝DF，∠EDF＝60°
∵△DMN为等边三角形
∴∠MDN＝60°，DM＝DN
∴∠MDN-∠NDF＝∠EDF-∠NDF，
即：∠MDF＝∠NDE∴△NDE≌△MDF
∴EN＝MF，∠DEN＝∠DFM＝60°
∴∠CEN＝60°
∴点F在直线NE上
（3）成立证明：如图，连接DE、DF，则DE、DF是三角形的中位线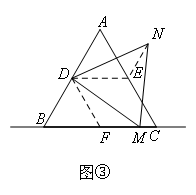
∴DE＝BC，DF＝AC，△BDF、△ADE都是等边三角形
∴DE＝DF，∠EDF＝60°
∵△DMN为等边三角形
∴∠MDN＝60°，DM＝DN
∴∠MDN-∠MDE＝∠EDF-∠MDE，
即：∠NDE＝∠MDF
∴△NDE≌△MDF
∴EN＝MF，∠DEN＝∠DFM＝120°
∴∠AEN＝60°
∴点F在直线NE上
知识点：四边形中的类比探究
略
略
WORD格式（
