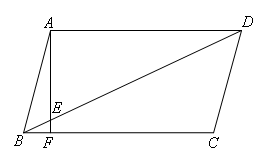
如图，在□ABCD中，∠ABC=75°，AF⊥BC于点F．AF交BD于点E，若DE=2AB，求∠AED的大小．
答案
证明：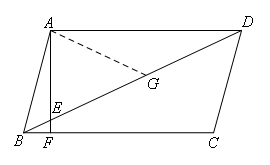
取DE的中点Ｇ，连接AG
∵AD∥BC，AF⊥BC
∴AF⊥AD
∴∠DAE=90°
∵G为DE中点
∴AG=GE=GD
∵DE=2AB
∴AB=AG=GD
∴∠ABG=∠AGB∠DAG=∠ADG
∵∠AGB=∠DAG+∠ADG
∴∠ABG=∠DAG+∠ADG=2∠ADG
∵AD∥BC
∴∠CBD=∠ADG
∴∠ABG=2∠CBD
∴∠ABC=3∠CBD=75°
∴∠ADG=∠CBD=25°
∴∠AED=90°-∠ADG=90°-25°=65°
知识点：中点问题
略
略
WORD格式（
