如图,在等腰梯形ABCD中,AB∥CD,AD=BC,AC和BD相交于点O,∠AOB=60 ,P,Q,R分别是AO,BC,DO的中点,求证:△PQR是等边三角形.
,P,Q,R分别是AO,BC,DO的中点,求证:△PQR是等边三角形.

答案
证明: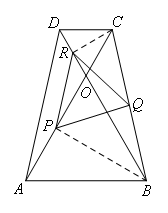
连接CR、BP
∵四边形ABCD是等腰梯形
∴AD=BC,∠DAB=∠CBA
∴△DAB≌△CBA
∴∠DBA=∠CAB
∵∠AOB=60![]()
∴△AOB是等边三角形
同理可得,△COD是等边三角形
∵P,R分别是AO,DO的中点
∴CR⊥OD,BP⊥OA,PR=![]() AD
AD
∴△BCR与△BCP均为直角三角形
∵Q是BC的中点
∴RQ=PQ=![]() BC
BC
∴RQ=PQ=PR,即:△PQR是等边三角形
知识点:中点问题
略
略








