慧慧在一次数学课上，将一副30°，60°，90°和45°，45°，90°的三角板如图放在直角坐标系中，发现点A的坐标刚好是（
，0），求图中两个三角板的交点P的坐标．
答案
解：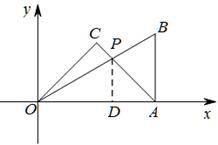
过点P作PD⊥x轴，垂足为点D设AD=x，在Rt△AOB和Rt△AOC中，
∵∠AOB=30°，∠OAC=45°
∴PD=AD=x，OD=
x
∵A（
，0）
∴OD+DA=，即x+x=
∴x=
即OD=9，PD=
∴点P的坐标为（9，）
知识点：坐标的应用
略
略
WORD格式（
