已知:如图,AB∥CD,∠EAF= ∠EAB,∠ECF=
∠EAB,∠ECF= ∠ECD.
∠ECD.
求证:∠AFC= ∠AEC.
∠AEC.

答案
证明:
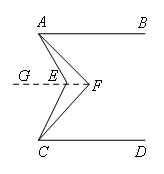
如图,过点F作FG∥AB,设∠EAF=α,∠ECF=β,
∵AB∥CD
∴FG∥CD
即FG∥AB∥CD
∴∠BAF=∠AFG,∠FCD=∠GFC
∵∠EAF=![]() ∠EAB,∠ECF=
∠EAB,∠ECF=![]() ∠ECD
∠ECD
∴∠EAB=4α,∠ECD=4β
∴∠BAF=3α,∠FCD=3β
∴∠AFC=∠AFG+∠GFC=∠BAF+∠FCD=3(α+β)
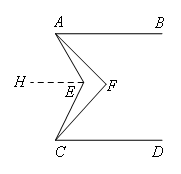
过点E作EH∥AB,
同理:∠AEC=∠AEH+∠CEH=∠BAE+∠ECD=4(α+β)
∴∠AFC=![]() ∠AEC
∠AEC
知识点:与角有关的辅助线
略
略








