如图1，在平面直角坐标系中，直线y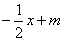＝（m>0）与x轴，y轴分别交于点A，B，过点A作x轴的垂线交直线y＝x于点D，C点坐标（m，0），连接CD．
（1）求证：CD⊥AB；
（2）连接BC交OD于点H（如图2），求证：DH＝BC．

图1

图2

答案

解：（1）由题意知：A（2m，0），B（0，m）
∵AD⊥x轴，点D在直线y＝x上
∴D（2m，2m）
∵C（m，0）
∴k_CD＝＝2
∵k_AB＝
∴k_CD·k_AB＝-1
∴CD⊥AB
（2）∵B（0，m），C（m，0）
∴OB＝m，OC＝m
∴BC＝
∵k_BC＝-1，k_OD＝1
∴k_BC·k_OD＝-1
∴BC⊥OD
∴OH＝
∵D（2m，2m）
∴OD＝
∴DH＝OD-OH＝
∴DH＝BC