如图，一次函数y＝的函数图象与x轴、y轴分别交于点A，B，以线段AB为直角边在第一象限内作Rt△ABC，且使∠ABC＝30°．
（1）求△ABC的面积；
（2）如果在第二象限内有一点P（m，），试用含m的代数式表示△APB的面积，并求当△APB与△ABC面积相等时m的值；
（3）在坐标轴上是否存在一点Q，使△QAB是等腰三角形？若存在，请直接写出点Q所有可能的坐标；若不存在，请说明理由．

答案

解：（1）由条件知：A（1，0），B（0，）
∴在Rt△ABO中，AB＝
在Rt△ABC中，
∵∠ABC＝30°
∴AC＝＝
∴S_△ABC＝
（2）S_{四边形POAB}＝S_△OBP＋S_△AOB
∵S_△OBP＝·（-m）·＝-m
S_△AOB＝·1·＝
∴S_{四边形POAB}＝-m＋
∵S_△AOP＝·1·＝
∴S_△APB＝S_{四边形POAB}-S_△AOP＝-m＋（m＜0）
当S_△APB＝时
-m＋＝
即m＝
（3）存在．

Q₁（-1，0），Q₂（3，0），Q₃（0，-）
提示：以A为圆心，AB长为半径作圆，分别交坐标轴于点Q₁，Q₃，Q₂．则Q₁A＝Q₂A＝2，由A点坐标可知Q₁、Q₂坐标．连接AQ₃，则△BAQ₃为等腰三角形，由三线合一可得Q₃点坐标．

Q₄（0，2＋），Q₅（0，）
提示：以点B为圆心，AB长为半径作圆，交y轴于点Q₄，Q₅（因为△ABQ₁为等边三角形，则其与x轴交点即为Q₁，A）．由BQ₄＝BQ₅＝2，结合B点坐标，可得Q₄，Q₅坐标．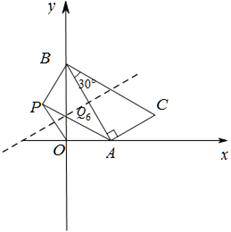

Q₆（0，）
提示：作AB的垂直平分线交y轴于点Q₆（因为△ABQ₁为等边三角形，则其与x轴交点即为Q₁）．由垂直平分线性质，可以在Rt△AQ₆O中，利用∠Q₆AO＝30°，求得OQ₆的长，即得点Q₆坐标．

知识点：一次函数存在性  

略

略

下载次数：2

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>