如图，在平面直角坐标系中，直线l₁：y＝分别与x轴、y轴交于点B，C，且与直线l₂：y＝交于点A．
（1）求出点A，B，C的坐标；
（2）若D是线段OA上的点，且△COD的面积为12，求直线CD的函数表达式；
（3）在（2）的条件下，设P是射线CD上的点，在平面内是否存在点Q，使以O，C，P，Q为顶点的四边形是菱形？若存在，直接写出点Q的坐标；若不存在，请说明理由．

答案

解：（1）∵y＝分别与x轴、y轴交于点B，C
∴C（0，6），B（12，0）
∵A为直线l₁、l₂交点
∴联立：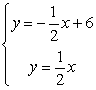
解得：
即A（6，3）
（2）设D（x，）
则S_△COD＝·6＝3x＝12
∴x＝4
∴D（4，2）
设直线CD表达式为：y＝kx＋b，将C、D坐标代入得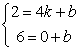

解得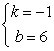
∴y＝-x＋6
（3）存在．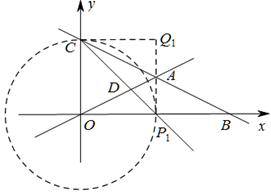

Q₁（6，6）
提示：以点O为圆心，OC长为半径作圆，与射线CD交于点P₁，把△P₁OC沿P₁C翻折，得到△P₁Q₁C,则Q₁即为所求．因为直线CD斜率为-1，所以∠OCD＝45°，P₁即为射线CD与x轴交点．此时菱形为正方形．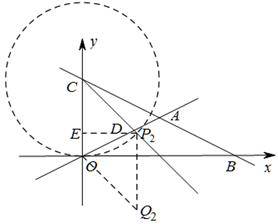

Q₂（，-）
提示：以点C为圆心，CO长为半径作圆交射线CD于P₂点，将△OCP₂沿OP₂翻折得到△OQ₂P₂，则Q₂点即为所求．过P₂向y轴做垂线，交y轴于点E，则△CEP₂是等腰直角三角形，可以得P₂坐标，再由P₂Q₂∥OC，且P₂Q₂＝OC，可得Q₂坐标．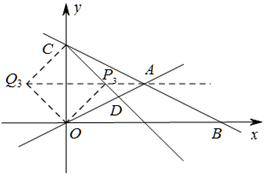

Q₃（-3，3）
提示：作线段OC的垂直平分线交射线CD于点P₃，将△OCP₃沿OC翻折得到△OCQ₃，则Q₃点即为所求．此时菱形为正方形．可得Q₃点坐标．

知识点：一次函数存在性  

略

略

下载次数：4

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>