已知：如图，在直角梯形COAB中，OC∥AB，以O为原点建立平面直角坐标系，A，B，C三点的坐标分别为A（8，0），B（8，10），C（0，4），点D为线段BC的中点，动点P从点O出发，以每秒1个单位的速度，沿折线OAB的路线移动，移动的时间为t秒．
（1）求直线BC的解析式；
（2）若动点P在线段OA上移动，当t为何值时，四边形OPDC的面积是梯形COAB面积的？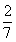
（3）动点P从点O出发，沿折线OAB的路线移动过程中，设△OPD的面积为S，请直接写出S与t的函数关系式，并指出自变量t的取值范围．
      （备用图）                     

答案

解：（1）设直线BC解析式为y=kx+b
∵B（8，10），C（0，4）在直线BC上
∴，解得
∴y=
（2）
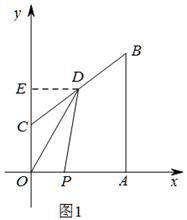
如图1，过点D作DE⊥y轴于点E
∵P在OA上运动
∴
∵D是BC中点，B（8，10），C（0，4）
∴D（4，7）
∴DE=4，CE=3
∵OP=t
∴=
∵=6
∴=-=
∵==56
∴==16即t=
（3）（i）如图1，当P在OA上时，即0≤t≤8
∴==

（ii）如图2，当P在AB上时，即8＜t≤18
∵AP=t-8，BP=18-t
∴=4t-32，=36-2t
∴=---=-2t+44

知识点：一次函数动点问题  

略

略

下载次数：3

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>