直线与坐标轴分别交于A，B两点，动点P，Q从O点出发，同时到达A点，运动停止．点Q沿线段OA运动，速度为每秒1个单位长度，点P沿路线O→B→A运动．
（1）直接写出A，B两点的坐标；
（2）设点Q的运动时间为t（秒），△OPQ的面积为S，求出S与t之间的函数关系式；
（3）当S=时，求出点P的坐标，并直接写出以点O，P，Q为顶点的平行四边形的第四个顶点M的坐标．

答案

解：(1)A（8,0）,B(0,6)(2)
（2）∵OA=8，OB=6
∴AB=10
∵点Q由O到A的时间是8ｓ
∴点P的速度是=2
当P在线段OB上运动时，0≤t≤3
OQ=t，OP=2t
∴S=

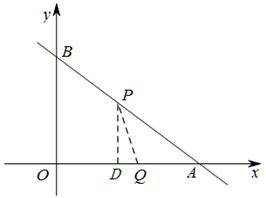
当P在线段BA上运动时，3＜t≤8
OQ=t，AP=16-2t
如图，过点P作PD⊥OA于点D
∴PD=
∴S=
综上可得：
（3）当P在线段OB上运动时，0≤t≤3
由S=可得：=
∴t=
∵＞3
∴此时不存在
当P在线段BA上运动时，3＜t≤8
由S=可得：
∴t=4
此时AP=8
∴PD=
AD=
∴OD=
∴点P的坐标为（，）
当以点O，P，Q，Ｍ为顶点的四边形是平行四边形时，画出图形如下所示：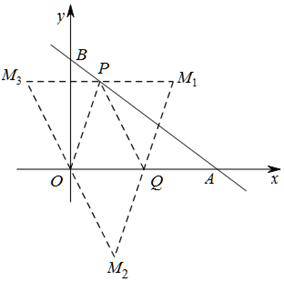

根据平行四边形的性质，可知点M的坐标为：（），（），（）

知识点：一次函数动点问题  

略

略

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>