如图,抛物线与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)以B、C、D为顶点的三角形是直角三角形吗?请证明你的结论.
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,请求出点P的坐标;若不存在,请说明理由.

答案
(1)由A(-1,0),B(3,0),C(0,-3)可得解析式:![]()
∴顶点D(1,-4)
(2)以B、C、D为顶点的三角形是直角三角形,理由如下:
过点D分别作x轴、y轴的垂线,垂足分别为E、F.
在Rt△BOC中,OB=3,OC=3,∴BC=![]() ,
,
在Rt△CDF中,DF=1,CF=OF-OC=4-3=1,∴CD=![]() ,
,
在Rt△BDE中,DE=4,BE=OB-OE=3-1=2,∴BD=![]() ,
,
∴BC2+CD2=BD2,故△BCD为直角三角形.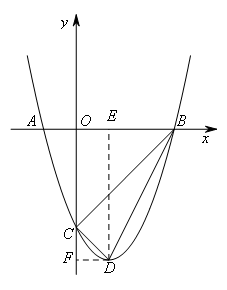
(3)存在;理由:连接AC,则易证Rt△AOC∽Rt△DCB,
∴∠CDB=∠OAC,∠DBC=∠ACO
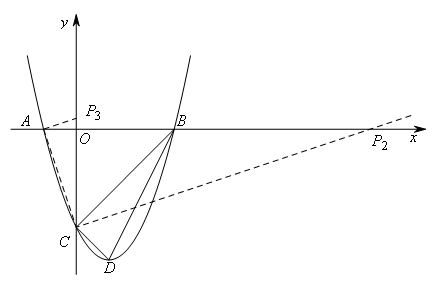
①当P在x轴上时,若∠APC=90°,则PC⊥x轴,
∴P与O重合,此时Rt△APC∽Rt△DCB,符合题意,∴P1(0,0)
若∠ACP=90°,∵∠CDB=∠OAC,易证Rt△APC∽Rt△DCB,符合题意,
∴Rt△AOC∽Rt△ACP,
∴![]() ,
,
∴OP=9,
∴P2(9,0)
②当P在y轴上时,若∠APC=90°,P与O重合,
若∠PAC=90°,∵∠DBC=∠ACO,
易证Rt△DCB∽Rt△PAC,符合题意,易证Rt△POA∽Rt△AOC,
∴![]() ,
,
∴OP=![]() ,
,
∴P3(0,![]() )
)
综上所述符合条件的P点有三个:P1(0,0),P2(9,0),P3(0,![]() )
)
知识点:二次函数综合题
略
略








