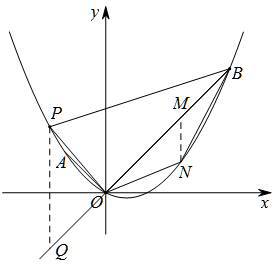
如图，平面直角坐标系xOy中，点A的坐标为(-2，2)，点B的坐标为(6，6)，抛物线经过A、O、B三点，连接OA、OB．
（1）求抛物线的解析式；
（2）点N是抛物线上位于直线OB下方的一个动点，求△BON面积的最大值，并求出此时点N的坐标；
（3）点P是抛物线上直线OB上方一点，求使得△BOP的面积与△BON的最大面积相等时的P点坐标．
答案
解：（1）将A(-2，2)，B(6，6)，O（0，0）得抛物线解析式：
（2）设N（n，
），过N作NM∥y轴，交OB于点M，
由O，B两点坐标知直线OB：y=x，
则M（n，n），MN=n-()
∴
∴当n=3时，
，此时N（3，
）
（3）设P（m，
），过P作PQ∥y轴，交直线OB于点Q，则Q（m，m）
∴
∵
∴
∴
∴
知识点：二次函数综合题
略
略
WORD格式（
