如图1，抛物线y＝mx2－11mx＋24m(m＜0)与x轴交于B、C两点（点B在点C的左侧），菱形OACD的顶点A也在抛物线上，且∠BAC＝90°．
（1）OB＝，OC＝，A点坐标为（，）D点坐标为（，）
（2）设垂直于x轴的直线l：x＝n与抛物线交于点M，与CD交于点N，若直线l沿x轴方向左右平移，且交点M始终位于抛物线上A、C两点之间．设MN的长度为y1，请用含n的代数式来表示y1．
（3）在（2）的情况下，试探究：当n为何值时，四边形AMCN的面积取得最大值，并求出这个最大值．
答案
解：（1）令y=0，可得mx2－11mx＋24m=0，可求得，B（3，0），C（8，0）.
连接AD，则AD⊥BC于点E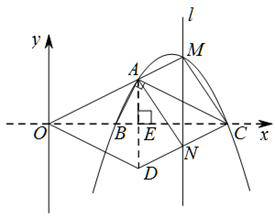
由菱形对角线互相垂直且平分可知，E为OC中点，则E（4，0），A、D关于x轴对称.
∵△AEB∽△CEA，
∴
，
又∵BE=1，EC=4，
∴AE=2，A（4，2），D（4，－2）
（2）由A点坐标可知抛物线解析式为
．
由C、D点坐标可知直线CD解析式：
由此可得M
，N（
）．
则
（4＜n＜8）
即
（4＜n＜8）．
（3）S四边形AMCN=S△AMN+S△CMN=
=
=
（4＜n＜8）
∴当n=5时，面积最大为9．
知识点：二次函数综合题
略
略
WORD格式（
