如图，已知点A（-1，0），B（4，0），点C在y轴的正半轴上，且∠ACB=90°，抛物线经过A、B、C三点．

（1）求抛物线的解析式；
（2）在抛物线上是否存在点N，使得？如果存在，请求出点N的坐标；如果不存在，请说明理由．

答案

解：（1）要求抛物线解析式，只需再求出点C坐标即可，即求OC长度.
∵∠ACB=90°，CO⊥AB，
∴△ACO∽△CBO．则,
又∵AO=1,OB=4,
∴CO=2.
由A（-1，0），B（4，0）、C（0，2）三点坐标求得解析式：
（2）∵,
∴△BCN中BC边上的高为．
如图，过点C作CD⊥CB，使CD为，
则符合条件的点D在直线BC两侧各有一个，分别标记为D₁，D₂.
由于平行线间的距离处处相等，所以点N一定在过点D的BC平行线上.
过点D₁，D₂作BC的平行线，分别交抛物线于点N₁，N₂，N₃.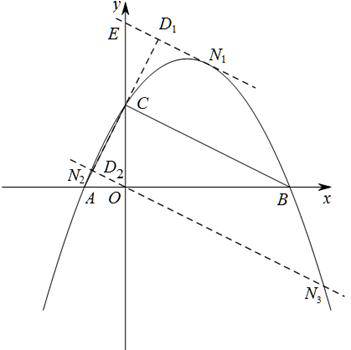

由CD₁=，△CD₁E∽△COA，可知，.
可得CE=2，E点坐标为（0，4）
由B、C两点坐标可得，直线BC：.
又∵EN₁∥CB,
∴EN₁：．
同理可求得，N₂N₃：．
联立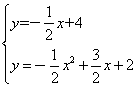
可求得N₁（2，3）
联立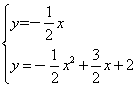
可求得N₂，N₃．
综上所述：存在N₁（2，3），N₂N₃．

知识点：二次函数综合题  

略

略

下载次数：4

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>