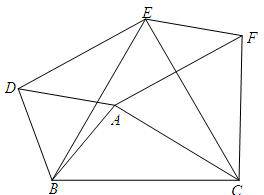
如图，分别以普通△ABC的三边为边在BC的同一侧分别作三个等边三角形，即△ABD、△BCE、△ACF.证明：四边形AFED是平行四边形

答案

解：四边形AFED是平行四边形，理由是：
∵△ABD、△BCE、△ACF为等边三角形
∴CB=CE，CA=CF，∠BCE=∠ACF=60°，
∴∠BCE-∠ACE=∠ACF-∠ACE，即∠BCA=∠ECF，
∴△ABC≌△FEC，
∴AB=EF，
又∵AB=AD，
∴AD=FE，
同理可证△ABC≌△DBE，ED=FA，
∴四边形AFED是平行四边形.

知识点：等边三角形的性质  平行四边形的判定  

略

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>