如图1，矩形OABC中，AB=8，OA=4，把矩形OABC折叠，使点B与点O重合，点C移到点F位置，折痕为DE.

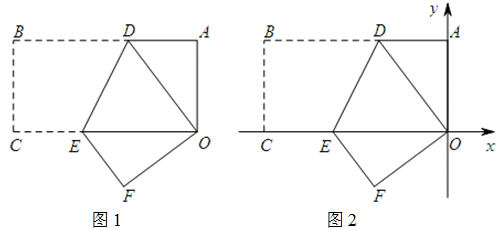
（1）求OD的长；
（2）如图2，以O点为坐标原点，OC，OA所在的直线分别作为x轴、y轴，建立平面直角坐标系，求直线DE的函数表达式，并判断点B关于x轴对称的点B′是否在直线DE上？

答案

解：（1）如图1，由折叠可得：OD=DB，
设OD=x，则DB=x，AD=8-x，
在Rt△AOD中，OA=4，
∴OD²=AD²+OA²，即x²=（8-x）²+4²，
解得x=5，
所以OD的长为5.
（2）由（1）得：AD=8-5=3，
∴D（-3，4）
由折叠可知∠BDE=∠ODE
∵AB∥CO
∴∠BDE=∠OEDOD=OE=5，
∴E（-5，0），
设直线DE的关系式为y=kx+b，则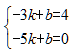
解得
∴直线DE为y=2x+10，点B关于x轴对称的点B′的坐标为
（-8，-4），
∵把x=-8代入y=2x+10，得：y=-6≠-4，
∴点B′不在直线DE上.

知识点：一次函数图象上点的坐标特征  勾股定理  一次函数表达式的确定  

略

略

下载次数：5

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>