如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别是D和E,AD,CE交于点H,EB=EH,求证:△BEC≌△HEA

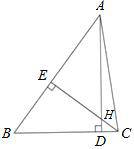
证明:∵AD⊥BC
∴∠ADB=90°
∴∠B+∠BAD=90°
∵CE⊥AB
∴∠AEH=90°
∴∠AHE+∠BAD=90°,∠AEH=∠ADB
∴_________________
在△BEC与△HEA中___________________
∴△BEC≌△HEA_________
①∠B=∠BAD,
②∠B=∠AHE,
③,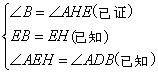
④,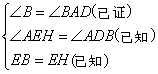
⑤ASA,
⑥AAS,
题目中空缺部分依次填写正确的选项是()

• A.①③⑤
• B.②④⑥
• C.②④⑤
• D.②③⑤

答案

正确答案：D

知识点：全等三角形的判定  

略

略

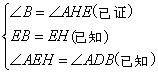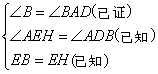下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>