已知:AB=AC,AD=AE,AF⊥BD交BD延长线于F,AG⊥CE交CE的延长线于G,求证:△AGC≌△AFB.
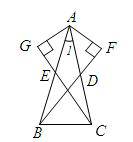
证明:在△ABD与△ACE中
∴
∴∠ABF=∠ACG(全等三角形对应角相等)
∵AF⊥BD,AG⊥CE
∴∠F=∠G=90°
在△AGC与△AFB中
∴
① ,②
,② ,③
,③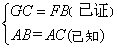 ,④
,④ ,⑤△ABD≌△ACE(SAS),⑥△ABD≌△ACE(AAS),⑦△AGC≌△AFB(AAS),⑧△AGC≌△AFB(ASA),⑨△AGC≌△AFB(HL),
,⑤△ABD≌△ACE(SAS),⑥△ABD≌△ACE(AAS),⑦△AGC≌△AFB(AAS),⑧△AGC≌△AFB(ASA),⑨△AGC≌△AFB(HL),
以上空缺处依次填写正确的选项是()
- A.①⑤③⑨
- B.②⑥④⑦
- C.①⑤④⑦
- D.②⑥④⑥
答案
正确答案:C
略
略








 ,②
,② ,③
,③ ,⑤△ABD≌△ACE(SAS),⑥△ABD≌△ACE(AAS),⑦△AGC≌△AFB(AAS),⑧△AGC≌△AFB(ASA),⑨△AGC≌△AFB(HL),
,⑤△ABD≌△ACE(SAS),⑥△ABD≌△ACE(AAS),⑦△AGC≌△AFB(AAS),⑧△AGC≌△AFB(ASA),⑨△AGC≌△AFB(HL),