目前，“低碳”已成为保护地球环境的热门话题，某高科技发展公司投资500万元，成功研制出一种市场需求量较大的低碳高科技产品，再投入资金1500万元作为固定投资．已知生产每件产品的成本是40元，在销售过程中发现：当销售单价定为100元时，年销售量为20万件；销售单价每增加10元，年销售量将减少1万件，设销售单价为x（元），年销售量为y（万件），年获利为z（万元）．（年获利=年销售额－生产成本－投资）
（1）试写出z与x之间的函数关系式．
（2）请通过计算说明到第一年年底，当z取最大值时，销售单价x应定为多少，此时公司是盈利了还是亏损了？
（3）若该公司计划到第二年年底获利不低于1130万元，请借助函数的大致图象说明第二年的销售单价x（元）应确定在什么范围．

答案

解：(1)依题意知,当销售单价定为x元时,年销售量减少(x100)万件,y＝20(x100)=x+30 .
由题意,得z=(30x)(x40)5001500=x²+34x3200.
即z与x之间的函数关系是z=x²+34x3200.
(2)∵z=x²+34x3200=(x170)²310.
∴当x=170时，z取最大值为310,即当z取最大值310万元时，销售单价应定为170元.到第一年年底公司还差310万元才能收回全部投资，所以此时公司是亏损了．
(3)由题意知，第二年的销售单价定为x元时，年获利为:z=(30x)(x40)310=x²+34x1510.
当z=1130时，即1130=x²+34x1510，整理得x²340x+26400=0,
解得:x₁=120，x₂=220.
函数z=x²+34x1510的图象大致如图所示,

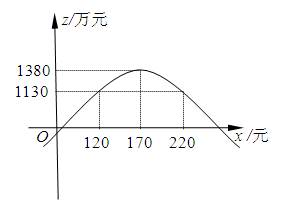
由图象可以看出:当120≤x≤220时，z≥1130.
故第二年的销售单价应确定在不低于120元且不高于220元的范围内.

知识点：函数类应用题  

略

略

下载次数：4

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>