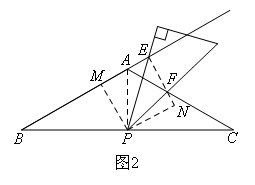
等腰△ABC,AB=AC=8,∠BAC=120°,P为BC的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在点P,三角板绕P点旋转.(1)如图1,三角板两边分别交AB,AC于点E,F时,求证:△BPE∽△CFP;(2)操作:将三角板绕点P旋转到图2的情形时,三角板的两边分别交BA的延长线、边AC于点E,F.①探究1:△BPE与△CFP还相似吗?(只需写出结论)②探究2:连接EF,△BPE与△PFE是否相似?请说明理由.③设EF=m,△EPF的面积为S,试用含m的代数式表示S.

答案
(1)证明:∵AB=AC,∠BAC=120°
∴∠B=∠C=30°
∵∠EPF=30°
∴∠BPE+∠CPF=150°
∵∠BPE+∠BEP=150°
∴∠CPF=∠BEP
∴△BPE∽△CFP
(2)解:①相似②相似,理由如下:
∵△BPE∽△CFP
∴![]()
∵BP=CP
∴![]()
∵∠B=∠EPF
∴△BPE∽△PFE
③连接AP,过P作PM⊥AB、PN⊥EF,分别交AB,EF的延长线于点M,N.
∵AB=AC,P为BC的中点
∴AP⊥BC由(1)得:∠B=30°
∴BP=![]()
∵PM⊥AB
∴PM=![]()
由上问知:△BPE∽△PFE
∴∠BEP=∠PEF
∴EP是∠BEF的平分线
∴PM=PN=![]()
∴S△EPF=![]() =
=![]() =
=![]()
知识点:相似综合模型
略
略








