在△ABC中，AD⊥BC于D，∠B=2∠C，求证：CD=AB+BD．
   

答案

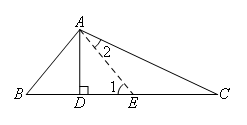
证明：如图，在线段DC上截取DE，使DE=BD，连接AE．
      ∵AD⊥BC
      ∴∠ADB=∠ADE=90°
      在△ABD和△AED中
       
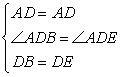
      ∴△ABD≌△AED（SAS）
      ∴∠B=∠1，AB=AE
      ∵∠B=2∠C
      ∴∠1=2∠C
      ∵∠1是△AEC的一个外角
      ∴∠1=∠C+∠2
      ∴∠C=∠2
      ∴AE=CE
      ∵CD=CE+ED
      ∴CD=AE+BD
      ∴CD=AB+BD
      （如果延长DB到点F，使BF=AB，连接AF也可进行证明）

知识点：三角形全等之截长补短  

略

略

下载次数：2

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>